Χρωματα εννεαδικου πινακα
Τα χρώματα του εννεαδικού πίνακα
Προ καιρού μιλήσαμε για τον χρωματισμό του εννεαδικού πίνακα, του βασικού πίνακα πάνω στον οποίο στηρίζονται οι σχηματισμοί των πρωταρχικών, των μικρότερων «μαγικών τετραγώνων», δηλαδή αυτών των τετραγώνων που διαιρούνται σε 9 μικρότερα τετράγωνα, όσοι είναι και οι 9 αριθμοί της μονάδας (ή αν προτιμάτε, οι 9 μονοί αριθμοί, χωρίς να συμπεριλαμβάνεται το μηδέν*).
*[Όχι πως η έννοια του μηδέν δεν ήταν κατανοητή από τα αρχαία χρόνια, αυτό δηλώνει και η αρχαιοελληνική ονομασία του «μηδέ εν» (= ούτε ένα), όμως το μηδέν σαν αριθμητικό σύμβολο, ικανό να συμμετέχει σε αριθμητικές πράξεις ανευρίσκεται για πρώτη φορά σε μια ινδική πραγματεία του 628 μ. Χ., που έγραψε ο τότε τριαντάχρονος ινδός μαθηματικός Βραχμαγκούπτα, που έγινε διευθυντής του αστεροσκοπείου του Ουτζέν.**

Ήδη εκείνη την εποχή η αναγκαιότητα του μηδέν ως τοποτηρητή που να εξασφαλίζει στα άλλα αριθμητικά ψηφία τη σωστή τους θέση ήταν γνωστή. Όμως ο Βραχμαγκούπτα στο βιβλίο του προχώρησε ένα βήμα παρακάτω. Για πρώτη φορά στην ιστορία έδωσε έναν ορισμό για το μηδέν. Έγραψε: «το μηδέν είναι το αποτέλεσμα της αφαίρεσης ενός αριθμού από τον εαυτό του».
Το βιβλίο των αριθμών, Peter J. Bentley
Κεφ. Η ΕΠΙΝΟΗΣΗ ΤΟΥ ΤΙΠΟΤΕ]
**(Κάνοντας λογοπαίγνιο, παίρνοντας την ονομασία Ουτζέν και ανταλλάσσοντας την προφορά του «τζ» σε «δ», το Ουτζέν γίνεται Ουδέν, άρα ο Βραχμαγκούπτα έγινε διευθυντής του αστεροσκοπείου του Ουδέν, δηλαδή του Μηδέν)
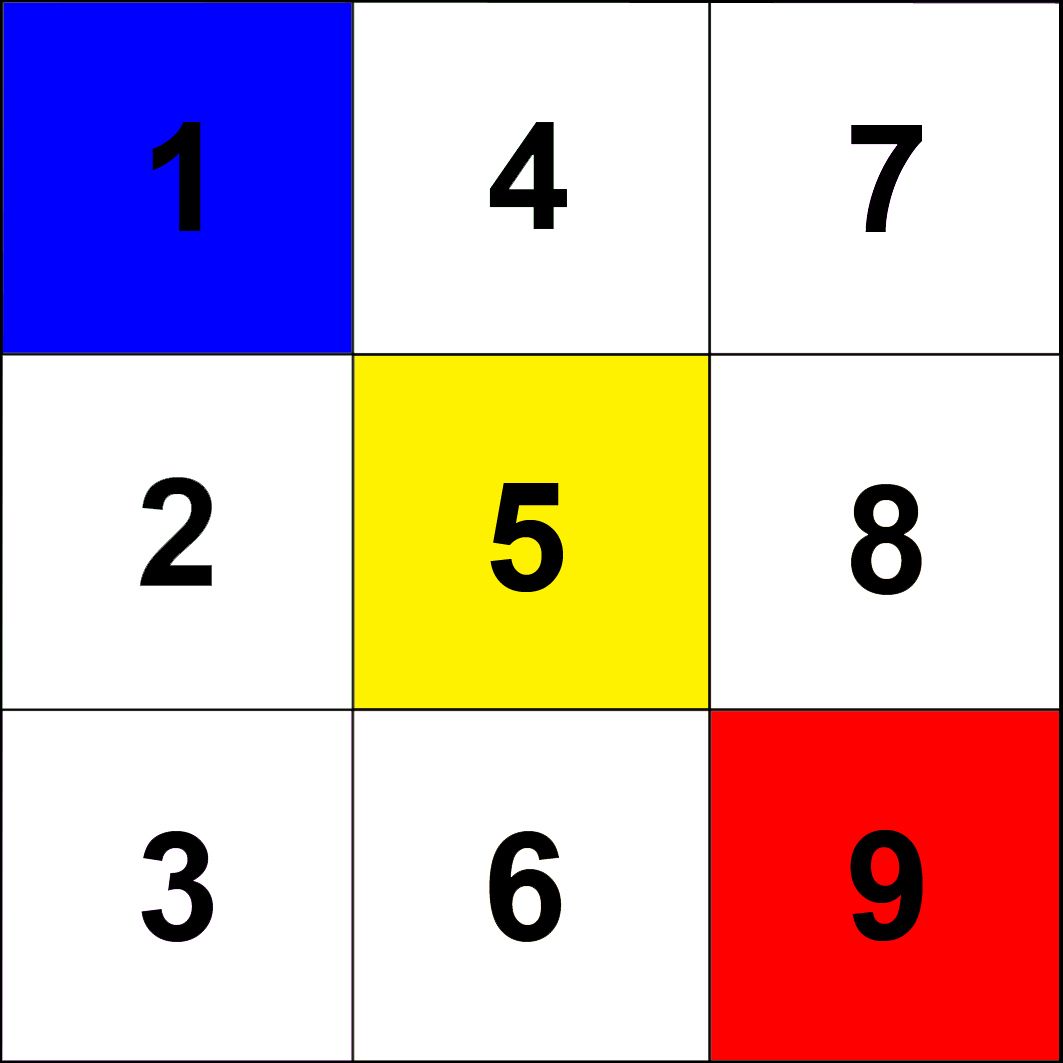
Προσέχοντας τον χρωματισμένο πλέον εννεαδικό πίνακα, παρατηρούμε πως τα 9 τετράγωνα που τον αποτελούν, καλύπτονται από 6 χρώματα, τα 6 χρώματα της ίριδας. Από τα τρία βασικά χρώματα του συστήματος αφαιρετικής μίξης (δηλ. των βαφών), ήτοι: μπλε, κίτρινο, κόκκινο και τα τρία παράγωγά τους χρώματα, ήτοι πράσινο, μωβ, πορτοκαλί.
Τα παράγωγα δε, καταλαμβάνουν έκαστο από δυο τετράγωνα.
Ενώ λοιπόν έχουμε ένα μπλε, ένα κίτρινο και ένα κόκκινο τετράγωνο, έχουμε από δυο πράσινα, δυο μωβ και δυο πορτοκαλί.
Αναλυτικότερα έχουμε την αντιστοιχία χρωμάτων – αριθμών ως εξής:
Μπλε 1
Κίτρινο 5
Κόκκινο 9
Πράσινο 2, 4
Μωβ 3, 7
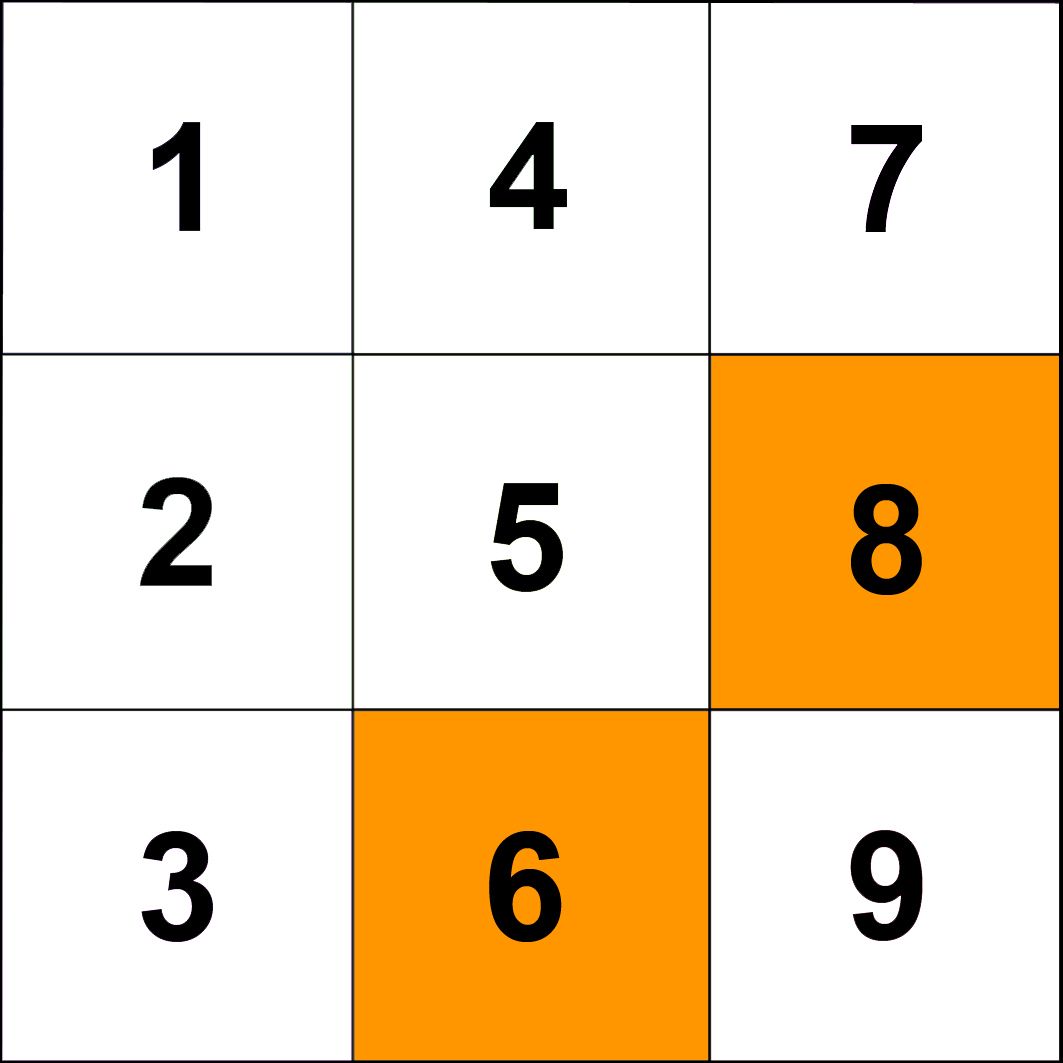
Πορτοκαλί 6, 8
Μια άλλη παρατήρηση μας αποκαλύπτει πως τα χρώματα που βρίσκονται στις αρχές των σειρών, δηλαδή τα αρχικά χρώματα κάθε σειράς, τόσο καθέτως, όσο και οριζοντίως είναι 3, τα εξής:
Μπλε, Πράσινο, Μωβ.
(καθέτως: 1 μπλε, 4 πράσινο, 7 μωβ
οριζοντίως: 1 μπλε, 2 πράσινο, 3 μωβ).
Επίσης, λόγω της ιδιότητάς τους σαν βασικά χρώματα, αλλά και σαν αντιστοιχίες των Αρχών Ψυχή και Ύλη, ενέχουν θέση αρχής τόσο το μεσαίο 5 κίτρινο (ψυχή), όσο και το τελευταίο 9 κόκκινο (ύλη) τετράγωνο.
Συμπεραίνουμε λοιπόν πως τα μόνα τετράγωνα που δεν ενέχουν θέση αρχής είναι τα δυο πορτοκαλί με τους αριθμούς 6 και 8.
Προτού προχωρήσουμε όμως, καλό είναι να ρίξουμε μια ματιά σε δυο παλαιότερες αναρτήσεις για να θυμηθούμε κάποια πράγματα για τις τριαδικότητες:
Πρωταρχική τριάδα στην δημιουργία θεωρείται η τριας Πνεύμα – Ψυχή – Ύλη, στην οποία αναλογικά μπορούμε να αντιστοιχήσουμε κάθε άλλη τριάδα, όπως βεβαίως και την τριάδα των βασικών χρωμάτων, όπου το Μπλε αντιστοιχεί στο Πνεύμα (αν σας διευκολύνει στην κατανόηση, μπορείτε να το αποκαλέσετε «ενέργεια»), το κίτρινο στην Ψυχή και το κόκκινο στην Ύλη.
(Αυτά ίσως σας γίνουν πιο κατανοητά διαβάζοντας το πιο κάτω άρθρο)
Έτσι λοιπόν, τα τρία βασικά χρώματα είναι χρώματα ΑΡΧΕΣ, αλλά όπως είδαμε πιο πάνω, θέση αρχής ενέχουν και δυο από τα τρία παράγωγα χρώματα, το πράσινο και το μωβ.
Όμως, τι ακριβώς σημαίνει ΑΡΧΗ;
Με το θέμα αυτό θα ασχοληθούμε σε επόμενο άρθρο.
Σ.σ.: Εάν θέλετε κάποιες διευκρινήσεις πάνω σε αυτά που αναφέρθηκαν, ή εάν θέλετε να εκθέσετε τις δικές σας απόψεις, παρακαλώ επικοινωνήστε μαζί μας γράφοντας στην στήλη DIALOGUE.
admin is | Topic: Uncategorized, μαγικά τετράγωνα | Tags: None




8 Comments, Comment or Ping
ΑΥΓΟΥΣΤΑ
Πάνο, ξέμπλεξέ με λίγο. Στον χρωματικό 9αδικό πίνακα: Το μπλε στο 1, κατεβαίνει και συναντά το κίτρινο του 2 και γίνεται πράσινο. Σωστά; Όντας πράσινο συνεχίζει για να συναντήσει το κόκκινο του 3 και γίνεται…..;;; Τι χρώμα γίνεται το πράσινο που συναντά το κόκκινο; Γιατί, δεν μπορώ να το ”ξεβάψω” και να το ξανακάνω μπλε για να το κατεβάσω στο 3! Το κατεβάζω ως πράσινο (ήδη δηλαδή επηρεασμένο)….
30-3-2015
admin
ΑΥΓΟΥΣΤΑ όντως τα έχεις μπλέξει. Ο χρωματισμός του 9δικού δεν γίνεται καταβάζοντας το ένα τετράγωνο στο από κάτω του. Ξαναρίξε μια ματιά στον “χρωματισμό των μαγικών τετραγώνων Β” https://xromata.com/?p=5999 για να δεις πως βγαίνουν τα χρώματα του πίνακα, εκτός κι αν εννοείς κάτι άλλο.
Πάνος
31-3-2015
Πάνος
ΑΥΓΟΥΣΤΑ ένα μεγάλο ΕΥΧΑΡΙΣΤΩ γιατί με αυτό το ερώτημά σου με έκανες να προβιβαστώ σε μεγαλύτερη τάξη.
Είδα πράγματα που ενώ τα κοίταζα χρόνια δεν τα “έβλεπα”.
Ό,τι γράφω παρακάτω γράφονται περισσότερο για εμένα, σαν σημειώσεις για μελλοντικές εργασίες.
Ναι μεν, φαινομενικά, οι αριθμοί στον εννεαδικό πίνακα έχουν την χρωματική τους θέση, αλλά δεν ταυτίζονται οπωσδήποτε και επακριβώς με το χρώμα της θέσης τους.
(Αυτό επάγεται και από άλλες χρωματικές διεργασίες επί του πίνακα, όπως η χρήση των χρωματικών ακτινοβολιών ή η μετατροπή του πίνακα σε κύβο).
Οι αριθμοί σαν ιδέες που είναι δεν έχουν μορφή. Τα σχήματα (τετράγωνα στην συγκεκριμένη περίπτωση) είναι μορφές. Τα χρώματα είναι και δεν είναι μορφές.
Εάν προσδιορίσουμε επιθετικά και όχι αριθμητικά τα 9 τετράγωνα, αναφερόμαστε σε 6 επιθετικούς προσδιορισμούς. Δηλαδή αν αντί να πούμε το τετράγωνο αρ. ένα, δύο κλπ. πούμε το πρώτο τετράγωνο (ένα και μοναδικό), το δεύτερο τετράγωνο (είτε οριζοντίως, είτε καθέτως), παρομοίως και το τρίτο τετράγωνο, μένει να το ποθετήσουμε το τέταρτο τετράγωνο (που θα λάβει την θέση είτε του τετραγώνου με αρ. 5, είτε του με αρ. 9), οπότε έχουμε το πέμπτο τετράγωνο (είτε οπιζοντίως, είτε καθέτως) και απομένει τέλος το ένα και μοναδικό έκτο τετράγωνο.
Αυτές και άλλες σκέψεις μου γεννήθηκαν σήμερα τέσσερεις τετάρτου (2Χ4) που όπως ξέρεις το 4 είναι αριθμός φθαρτός και θνητός (όπου φθορά σημαίνει εδώ “στροφή κατά της προσωρινής ζωικής μορφής” και ο θάνατος οδηγεί σε νέα γέννηση).
Επειδή δε το βιβλίο της φύσης είναι ο καλύτερος διδάσκαλος, στρώθηκα πρωί – πρωί στην εντομολογία για επιβεβαίωση των ανωτέρω περί 4.
Η πεταλούδα λοιπόν γεννιέται από το αυγό, γίνεται κάμπια, μεταμορφώνεται σε χρυσαλίδα (με άλλα λόγια ξαναμπαίνει στο αυγό, που αυτή την φορά είναι κουκούλι, για να ξαναγεννηθεί σαν πεταλούδα, και σ’ αυτό το 4ο στάδιο, να γεννήσει αυγά και να πεθάνει.
Όπως είπα, μην ασχοληθείς με αυτά τα πιθανόν δυσκολονόητα γραφόμενά μου. Απευθύνονται κυρίως σε μένα, σαν υπενθύμιση για μελλοντικές εργασίες που θα αναρτηθούν κάποτε σαν άρθρα εδώ.
Πάνος
4-4-2015
ΑΥΓΟΥΣΤΑ
Χαίρομαι με την χαρά σου και περιμένω στο μέλλον τις νέες σου εργασίες. Όσα γράφεις θα μου ήταν απολύτως κατανοητά, ΑΝ μπορούσα να καταλάβω και το σημείο του … ”επιθετικού προσδιορισμού” που αναφέρεις, αλλά …. μάταια.
Καλή συνέχεια.
Πάνος
ΑΥΓΟΥΣΤΑ αν και είπα πως ό,τι έγραψα ήταν σημειώσεις κυρίως για μένα, δεν μπορώ να μην σου εξηγήσω τί εννοώ με τους επιθετικούς προσδιορισμούς.
Τα 9 τετράγωνα του πίνακα αναφέρονται σαν: το τετράγωνο με τον αριθμό 1, το τετράγωνο με τον αρ. 2 και ούτω καθεξής.
Με τον επιθετικό προσδιορισμό αναφέρεται η θέση του τετραγώνου και όχι ο αριμός που εμπεριέχει.
Έτσι έχουμε το πρώτο τετράγωνο, το δεύτερο τετράγωνο, το τρίτο τετράγωνο κλπ.
Τα τακτικά αριθμητικά επίθετα φανερώνουν τη σειρά, δηλαδή τη θέση που έχει το ουσιαστικό για το οποίο γίνεται λόγος.
Στην περίπτωση του “δεύτερου” τετραγώνου, έχουμε δυο τοποθετήσεις δεύτερου τετραγώνου στον πίνακα. 1) το καθέτως δεύτερο τετράγωνο 2) το οριζοντίως δεύτερο τετράγωνο. Το ίδιο συμβαίνει και με τρίτο τετράγωνο.
Έγινα περισσότερο κατανοητός τώρα;
Πάνος
6-4-2015
ΑΥΓΟΥΣΤΑ
Δηλαδή, ο επιθετικός προσδιορισμός φανερώνει την θέση και τα τακτικά αριθμητικά επίθετα την σειρά. Οπότε δεν μας νοιάζει το πως κοιτάμε τον πίνακα. Σωστά;
6-4-2015
Πάνος
Όχι Αυγούστα! Πάλι μπερδεύτηκες.Τα τακτικά αριθμητικά είναι επιθετικοί προσδιορισμοί που δηλώνουν την θέση ή σειρά.
Το νόημα ήταν ότι οι αριθμοί δεν είναι πάντα ταυτόσημοι με το χρώμα του τετραγώνου το οποίο αριθμούν, δηλαδή το 2 δεν είναι οπωσδήποτε πάντοτε το ίδιο πράσινο χρώμα…..
Άσε το. Θα μας δοθεί η ευκαιρία να επανέλθουμε στο θέμα αυτό.
Τώρα, σχετικά με τον τελευταίο προβληματισμό σου για τα 5 δάχτυλα, ίσως σε βοηθήσει η μυθολογία να βρεις κάποια απάντηση.
Για βοήθημα λοιπόν σου δίδω αυτό:
*Ιδαίοι Δάκτυλοι: Τη φύλαξή του Δία είχαν αναλάβει οι Κουρήτες (ή οι Κορύβαντες, ή οι Ιδαίοι Δάκτυλοι) οι οποίοι χόρευαν οπλισμένοι έξω από το σπήλαιο κρούοντας τις ασπίδες και τα όπλα τους, προκειμένου να μην ακούσει ο Κρόνος το κλάμα του μωρού.
Οι Ιδαίοι Δάκτυλοι ήταν δαίμονες που κατάγονταν από την κρητική ή τη φρυγική Ίδη και ανήκαν στην ακολουθία της μητέρας των θεών Ρέας ή Κυβέλης.
Ο Στράβων αναφέρει ότι έλαβαν αυτή την ονομασία επειδή ήταν 5, όσοι και τα δάχτυλα του χεριού, ενώ ο Απολλόδωρος υποστηρίζει ότι ονομάστηκαν έτσι γιατί η μητέρα τους στήριξε τα δάχτυλά της στο χώμα, λίγο πριν τους γεννήσει, για να ανακουφιστεί από τους πόνους του τοκετού. Σύμφωνα με άλλη εκδοχή ονομάστηκαν Δάκτυλοι επειδή ήταν επιδέξιοι τεχνίτες.
Οι περισσότεροι αρχαίοι συγγραφείς παραδέχονται ότι ήταν 5, ενώ μερικοί υποστήριζαν ότι ήταν 10 (5 άντρες, 5 γυναίκες), ενώ άλλοι ανέβαζαν τον αριθμό τους σε 100. Κατά Στράβωνα, πρώτοι ανακάλυψαν και επεξεργάστηκαν το σίδερο και διέδωσαν τα Μυστήρια. Τους ταύτιζαν με τους Κουρήτες. Σύμφωνα με μια ηλειακή παράδοση οι Ιδαίοι ήταν 5, ο Ηρακλής, ο Παιωναίος, ο Επιμήδης, ο Ιάσιος και ο Ίδας. Ο μεγαλύτερος από αυτούς, Ηρακλής, πρότεινε στους υπόλοιπους να οργανώσουν αγώνα δρόμου, για να διασκεδάσουν τη μονοτονία τους. Έτσι, κατά τους Ηλείους, καθιερώθηκαν οι Ολυμπιακοί αγώνες.
Πάνος
10-4-2015
ΑΥΓΟΥΣΤΑ
Τώρα κατάλαβα!! επιθετικός προσδιορισμός και τακτικά αριθμητικά επίθετα είναι το ίδιο και φανερώνουν την θέση. ΟΚ. Είχα μπερδευτεί στο συντακτικό. Όσο για το χρώμα των τετραγώνων, αυτό σου έλεγα και εγώ. Ιδιαίτερα το 3 και το 7 δεν έχουν μόνο διαφορετική απόχρωση του ”μώβ” αλλά και τελείως άλλο χρώμα σε κάποιες περιπτώσεις, που φτάνει από το μαύρο μέχρι το λευκό!!
Ευχαριστώ και για το θέμα που μου έγραψες.
10-4-2015
Reply to “Χρωματα εννεαδικου πινακα”