Χρωματισμος μαγικων τετραγωνων (Β)
Ο χρωματισμός των μαγικών τετραγώνων (Β)
(συνέχεια)
Προ μηνός, περίπου, ξεκινήσαμε των χρωματισμό των μαγικών τετραγώνων. Για να ακριβολογούμε, τον χρωματισμό του εννεαδικού πίνακα, ο οποίος είναι η βάση των μαγικών τετραγώνων.
Την προηγούμενη φορά ασχοληθήκαμε κυρίως με την παρουσίαση του εννεαδικού πίνακα, την σχέση του και την διαφορά του με τα μαγικά τετράγωνα.
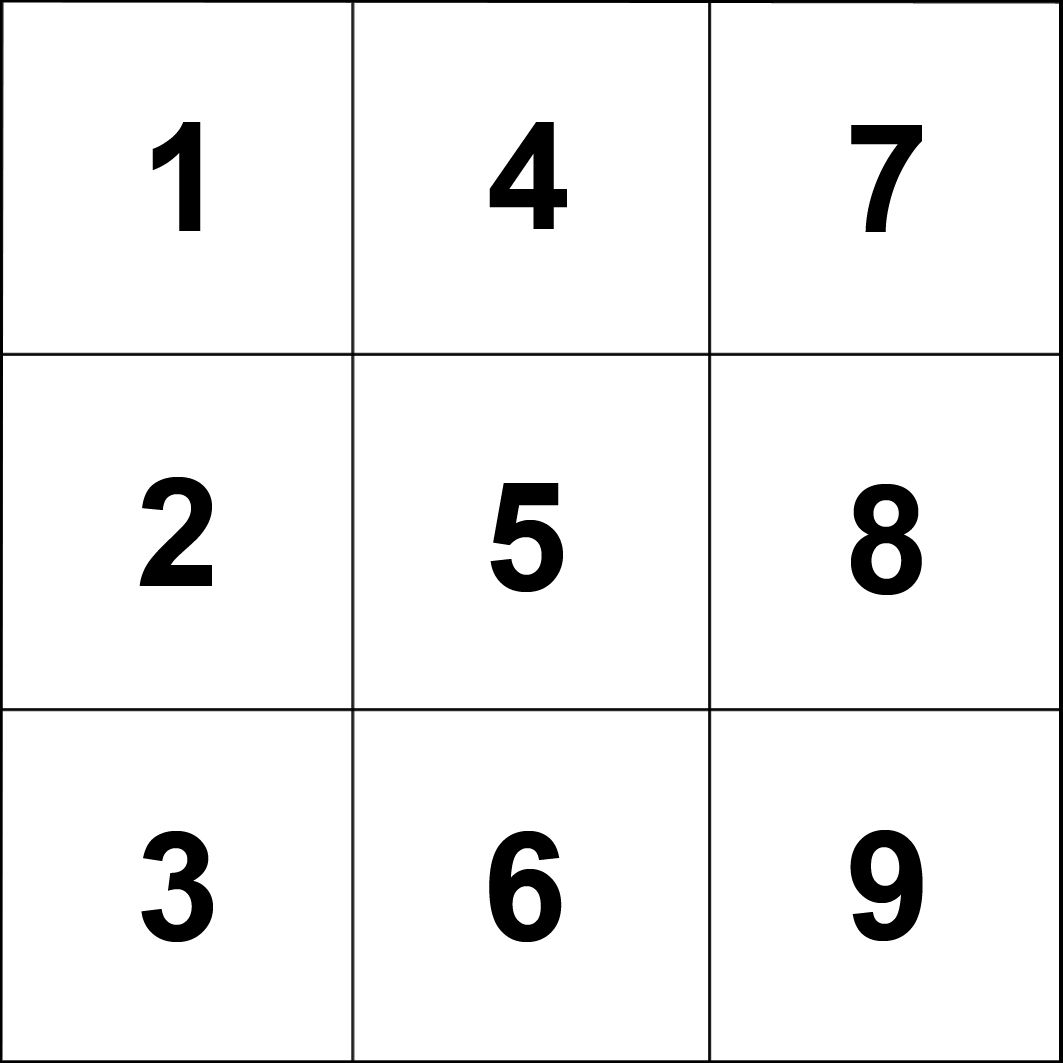
Επίσης αναφερθήκαμε στο ερώτημα που μου γεννήθηκε, γιατί δηλαδή ο συγκεκριμένος πίνακας αριθμείται καθέτως και όχι οριζοντίως, όπως θα ήθελα;

Στην δελεαστική πρόκληση να ερευνήσω το θέμα, σκέφθηκα ότι μόνο με απλοποίηση των 9 αριθμών ίσως μπορούσα να βγάλω κάποια άκρη, καταλήγοντας στο 3 και αναλογικά στα 3 βασικά χρώματα κι’ έτσι αποφάσισα να χρωματίσω τον εννεαδικό πίνακα με τα τρία βασικά χρώματα, δηλαδή τα μπλε, κίτρινο, κόκκινο.

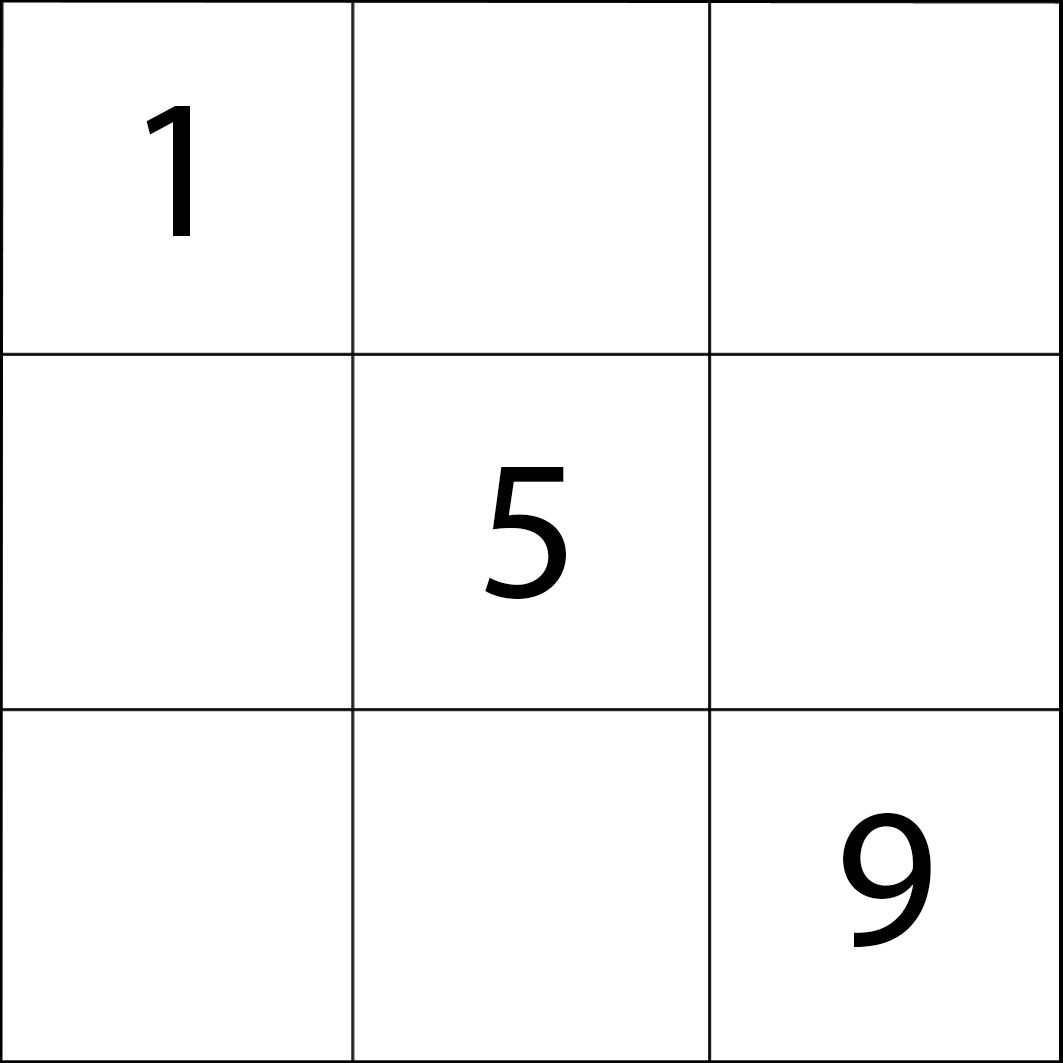
Πριν προχωρήσω στον χρωματισμό, βλέποντας τον εννεαδικό πίνακα αριθμημένο και καθέτως και οριζοντίως παρατηρώ ότι μόνο τρεις από τους εννέα αριθμούς παραμένουν σταθεροί στην ίδια θέση, οι αριθμοί 1, 5, 9 εκ των οποίων μόνο το 1 βρίσκεται στην αρχή, τόσο της πρώτης κάθετης στήλης, όσο και της πρώτης οριζόντιας, δηλαδή ενέχει θέση αρχής και στις δυο περιπτώσεις.
(Στο θέμα ΑΡΧΗ θα αναφερθούμε αργότερα).
Ξεκινώ παίρνοντας τα 9 τετραγωνάκια (δηλαδή τρεις σειρές τριών τετραγώνων) και τοποθετώ σε κάθε πρώτο τετράγωνο κάθε σειράς τον αριθμό 1. Σε κάθε δεύτερο (μεσαίο) τετράγωνο τον αριθμό 2 και σε κάθε τρίτο (τελευταίο) τετράγωνο κάθε σειράς τον αριθμό 3. Η διεργασία αυτή γίνεται και καθέτως και οριζοντίως και τελικά παρουσιάζεται η σχέση:
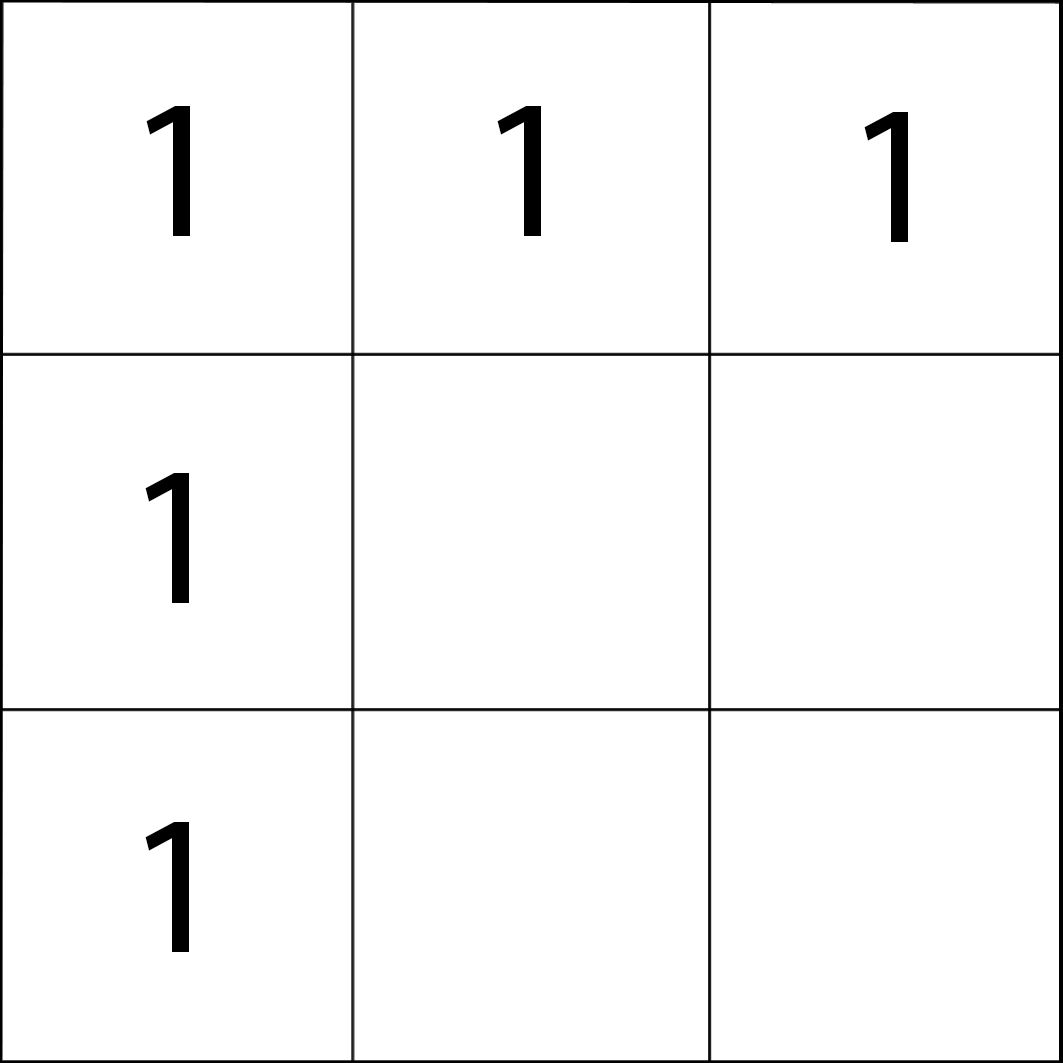
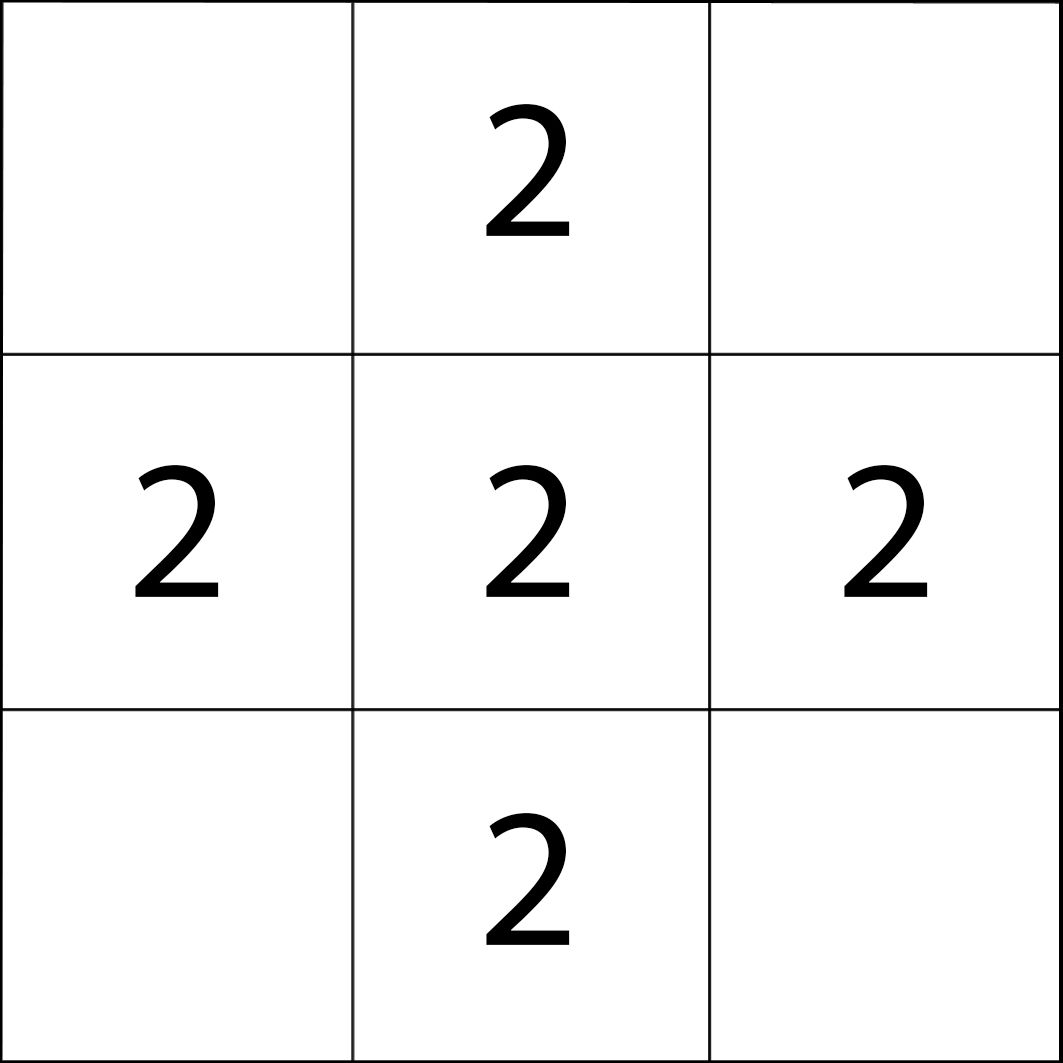
Αντιστοιχώ τον αριθμό 1 με το μπλε χρώμα και βάφω με μπλε χρώμα κάθε τετραγωνάκι που περιέχει τον αριθμό 1, δηλαδή το γάμα που σχηματίζεται με κορυφή την άνω (αριστερή όπως το κοιτώ) γωνία του τετραγώνου.

Παίρνω το κόκκινο χρώμα, που έχει τις αντίθετες ιδιότητες του μπλε χρώματος, και βάφω με αυτό το ακριβώς αντίθετα σχηματισμένο προς το μπλε γάμα, όπου δηλαδή ενυπάρχει ο αριθμός 3.

Τέλος, βάφω με κίτρινο χρώμα τα τετραγωνάκια που εμπεριέχουν τον αριθμό 2, δηλαδή τον σταυρό που σχηματίζουν όλα τα μεσαία τετραγωνάκια.

Γνωρίζοντας τις μίξεις των χρωμάτων βλέπω πως όπου έχω μπλε (1) με κίτρινο (2) προκύπτει πράσινο χρώμα, όπου μπλε (1) με κόκκινο (3) μωβ και όπου κόκκινο (3) με κίτρινο (2) έχω πορτοκαλί.
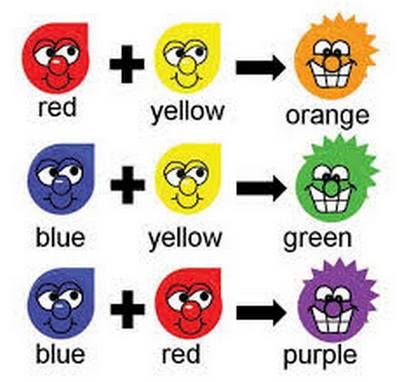

Βάζω ξανά τους 9 αριθμούς μέσα στα τετραγωνάκια, και καθέτως, όπως μου είχαν δοθεί και οριζοντίως, όπως ήθελα, και με έκπληξη βλέπω πως όπου τοποθετείται ο αριθμός 2, είτε οριζοντίως, είτε καθέτως, έχω πράσινο χρώμα, δηλαδή το ίδιο χρώμα και στις δυο περιπτώσεις.


Το ίδιο συμβαίνει και με τον αριθμό 4 που συμπίπτει και αυτός και στις δυο περιπτώσεις σε τετραγωνάκια με χρώμα πράσινο.
Αντιστοίχως, συμβαίνει το ίδιο και με τους αριθμούς 3 και 7 που μπαίνουν στα τετραγωνάκια με το μωβ χρώμα, αλλά και με τους αριθμούς 6 και 8 που έχουν χρώμα πορτοκαλί.

Ω! μαγικά τετράγωνα, όντως λειτουργείται μαγικά. Με τον χρωματισμό σας μου ξεκλειδώσατε ένα απέραντο πεδίο παρατηρήσεων και ερευνών!
(Για την «μαγεία» και την «Αρχή» θα μιλήσουμε λίαν συντόμως).
admin is | Topic: Uncategorized, Αριθμοί και χρώματα, Εξωλογισμοί, μαγικά τετράγωνα, Συμπαντικοί νόμοι και χρώματα | Tags: None

No Comments, Comment or Ping
Reply to “Χρωματισμος μαγικων τετραγωνων (Β)”