Μαγικα τετραγωνα
Τα μαγικά τετράγωνα
Σήμερα, η 20η Σεπτεμβρίου, είναι μια ιδιαίτερη προσωπική ημέρα για μένα, γι’ αυτό θέλησα να αναρτήσω την ημέρα αυτή, δηλαδή σήμερα, το άρθρο αυτό, με το οποίο ανοίγω μια σειρά βασισμένη στα «μαγικά τετράγωνα», ένα θέμα εξίσου σημαντικό για μένα και την πορεία μου στον κόσμο των χρωμάτων.
Ο χρωματισμός των μαγικών τετραγώνων ήταν αυτός που μου έδωσε την βεβαίωση πως κάτι, περίεργο, διαφορετικό, συμβαίνει με τα χρώματα και με ώθησε στην αναζήτηση και έρευνα των «μυστηρίων» τους.
Τα «μαγικά τετράγωνα» υπήρξαν για μένα «ο Διόνυσος»*, η πρωταρχική εκρηκτική ώθηση που εκπυρσοκροτεί, σου αλλάζει πορεία και σε στέλνει σε μαγευτικά ταξίδια άλλων κόσμων…..
*οὗτος δ᾽ ὁ δαίμων ὁ νέος, ὃν σὺ διαγελᾷς,
οὐκ ἂν δυναίμην μέγεθος ἐξειπεῖν ὅσος
καθ᾽ Ἑλλάδ᾽ ἔσται. δύο γάρ, ὦ νεανία,
τὰ πρῶτ᾽ ἐν ἀνθρώποισι·Δημήτηρ θεά—
γῆ δ᾽ ἐστίν, ……… ἀντίπαλον ὁ Σεμέλης γόνος
(Βάκχαι, Ευριπίδη)

Ένα άχρωμο άρθρο σε μια ιστοσελίδα με κύριο θέμα τα χρώματα!
Μια ανάρτηση χωρίς χρώματα (προς το παρόν) όσο κι αν φαίνεται περίεργο, έχει βασική θέση εδώ στα xromata.com γιατί αυτά, τα μαγικά τετράγωνα είναι υπαίτια για την βαθύτερη ενασχόλησή μου με τα χρώματα (κατ’ επέκταση και με την ύπαρξη αυτής της ιστοσελίδας) και έδωσαν αφορμή για πολλές έρευνες που ακολούθησαν.
Ας ξεκινήσουμε όμως από την αρχή και ας δούμε πρώτα τι είναι αυτά τα μαγικά τετράγωνα.
Σε εγκυκλοπαίδειες και λεξικά θα δούμε να αναγράφονται τα εξής ως εξήγηση των μαγικών τετραγώνων:
«Μαγικά τετράγωνα τάξης ν είναι τετραγωνικοί πίνακες με ν οριζόντιες αράδες τετραγώνων και ν κάθετες στήλες τετραγώνων με στοιχεία εντός αυτών ακέραιους αριθμούς από το 1 έως το τετράγωνο του ν, σε τέτοια διάταξη ώστε το άθροισμα των αριθμών (που εμπεριέχονται στα τετράγωνα) κάθε σειράς, οριζοντίως, καθέτως και διαγωνίως να είναι το ίδιο».
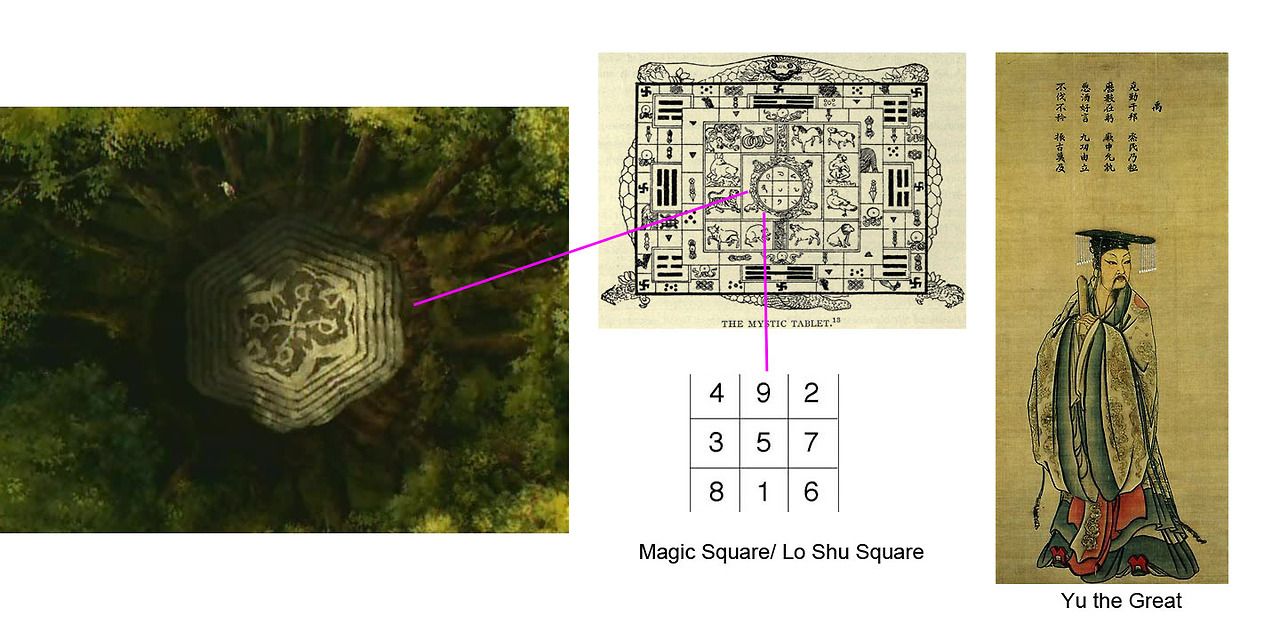
Το πρώτο μαγικό τετράγωνο που εμφανίστηκε στην ιστορία (2200 π. Χ.) είναι το αποκαλούμενο κινέζικο, που σύμφωνα με τον θρύλο ήταν το δώρο του Ουρανού προς τον μυθικό αυτοκράτορα Γιού. Ο Ουρανός έστειλε στον αυτοκράτορα το δώρο αυτό γραμμένο πάνω στο καβούκι μιας χελώνας που βγήκε από τον ποταμό Λο.

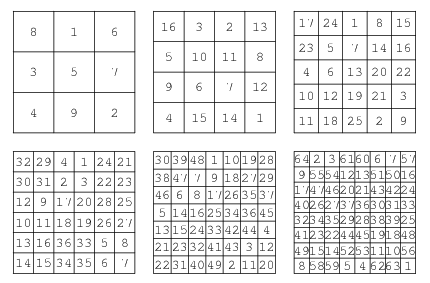
Το πρωταρχικό κινέζικο μαγικό τετράγωνο (ακριβέστερα: εσωτερική διαίρεση τετραγώνου σε μικρότερα τετράγωνα) είναι αυτό που διαιρείται σε 9 τετράγωνα (32 ), έκαστο των οποίων φέρει μέσα του έναν από τους 9 αριθμούς της μονάδας και έχει την εξής διάταξη (σχήμα) όπου όλα τα οριζόντια, κάθετα και διαγώνια αθροίσματα ισοδυναμούν με 15 (1+5 = 6)
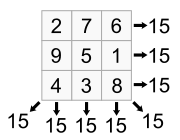
ήτοι: οριζοντίως 4 + 3 + 8 = 15
9 + 5 + 1 = 15
2 + 7 + 6 = 15
καθέτως 4 + 9 + 2 = 15
3 + 5 + 7 = 15
8 + 1 + 6 = 15
Διαγωνίως 4 + 5 + 6 = 15
2 + 5 + 8 = 15
Τα μαγικά τετράγωνα δεν έχουν πάψει μέχρι σήμερα να απασχολούν τους ενδιαφερόμενους. Μεγάλο ενδιαφέρον είχαν δείξει γι’ αυτά Ινδοί και Άραβες σοφοί, όμως ο βυζαντινός Μανουήλ Μοσχόπουλος απέκτησε τον τίτλο του «πατέρα» των μαγικών τετραγώνων, επειδή υπήρξε ο πρώτος που έγραψε βιβλίο γι’ αυτά.
Ο Μοσχόπουλος ήταν σπουδαίος βυζαντινός φιλόλογος και μαθηματικός. Έζησε από το 1265 έως το 1316 και έδρασε στην διάρκεια της βασιλείας του Ανδρόνικου Β΄. Ασχολήθηκε ιδιαίτερα με την κατασκευή «μαγικών τετραγώνων», μελέτησε τις ιδιότητές τους και έδωσε τους κανόνες σχηματισμού των.
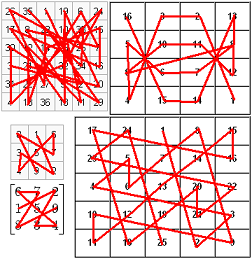
Δυο αιώνες περίπου μετά τον Μοσχόπουλο, κάποιος άλλος ασχολήθηκε με τα μαγικά τετράγωνα (ιδιαίτερα με αυτά της τάξης του 42 ) και παρέμεινε γνωστός και γι’ αυτήν την ιδιότητά του, ο Γερμανός αναγεννησιακός ζωγράφος Albrecht Durer, ο οποίος τα απεικόνισε μαζί με άλλα σύμβολα στον περίφημο χαρακτικό πίνακά του MELENCHOLIA.
Το χαρακτικό αυτό έργο του Ντύρερ δεν έχει χρώματα. Να υποθέσουμε ότι απέφυγε τον χρωματισμό της σύνθεσης αυτής επίτηδες, επειδή είναι πολύ δύσκολο να αποδώσεις σε κάθε σύμβολο τον σωστό χρωματισμό του;
Το ίδιο και οι πίνακες των μαγικών τετραγώνων. Παρουσιάζονται κι αυτοί άχρωμοι. Αποδίδονται μόνο με τετράγωνα και αριθμούς.
Τα στοιχεία που πληρούν τα μαγικά τετράγωνα είναι οι αριθμοί και έχουν μια αριθμοσοφική αξιολόγηση. Όμως τα «μαγικά τετράγωνα» πέρα από τις όντως δύσκολες αριθμοσοφικές τους αποκαλύψεις, μπορούν να αποκαλύψουν πολύ περισσότερα πράγματα εάν αντιστοιχιστούν οι αριθμοί τους με άλλα στοιχεία.
Κάτι ανάλογο έκανε ο Άγγλος John Searl στα μέσα του 20ου αιώνα όπου αντικατέστησε τους αριθμούς με μαγνήτες, και βρίσκοντας την κατάλληλη διάταξη τους προσπάθησε (και πέτυχε εν μέρει) να δημιουργήσει μια αεικίνητη ιπτάμενη μηχανή.
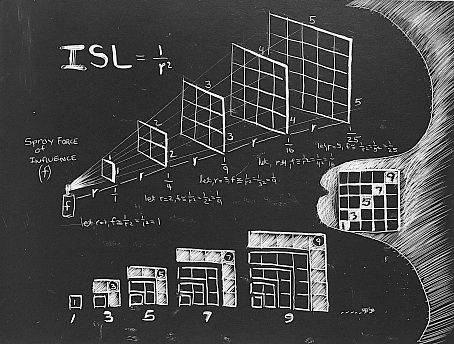

Τώρα θα μου πείτε, τι σχέση έχουν όλα αυτά (ιδίως τα άχρωμα μαγικά τετράγωνα) με τα χρώματα;
Το ερώτημά σας θα διευκρινιστεί λίαν προσεχώς, σε κάποια επόμενη ανάρτηση.
Επειδή όμως ο όρος «μαγικά» μας ανάγει αυτομάτως στην «μαγεία» και ίσως αναρωτηθήκατε γιατί τα τετράγωνα αυτά ονομάζονται «μαγικά» και ποια η σχέση τους με την μαγεία, θα κλείσουμε το άρθρο αυτό με την εξήγηση που δίνουν τα λεξικά για τον όρο «μαγεία».
ΜΑΓΕΙΑ: Το σύνολο των πράξεων, με την χρήση αντικειμένων ή λόγων, με τα οποία πιστεύεται ότι μπορεί κανείς να κάνει αόρατες δυνάμεις της φύσης να επιδράσουν για την επίτευξη επιθυμητού σκοπού.
admin is | Topic: Uncategorized, Αριθμοί και χρώματα, Εξωλογισμοί, μαγικά τετράγωνα, Συμπαντικοί νόμοι και χρώματα | Tags: None




No Comments, Comment or Ping
Reply to “Μαγικα τετραγωνα”