Αριθμητικες ιδιοτητες της τριαδας
Αριθμητικές Ιδιότητες της Τριάδας
Όπως είπαμε στο προηγούμενο άρθρο για το 3, τώρα θα ασχοληθούμε με τις αριθμητικές ιδιότητες αυτού του αριθμού.
Κάποιες από τις αριθμητικές ιδιότητες του τρίτου αριθμού τις έχουμε αναφέρει ξανά στο παρελθόν.
Εδώ τις έχουμε συγκεντρωμένες και μας προκαλούν τον θαυμασμό. ‘Εχουμε και λέμε λοιπόν:

Το 3 είναι ο πρώτος περιττός αριθμός.
Διαιρέτες του είναι: 1, 3
Το 3 είναι ο μόνος αριθμός που ισούται με το άθροισμα όλων των όρων κάτω από αυτόν. (3 = 2 + 1)
Είναι επίσης ο μόνος αριθμός του οποίου το άθροισμα του με τους αριθμούς που είναι κάτω από αυτόν ισούται με το γινόμενό τους. (1 + 2 + 3 = 1 x 2 x 3)
Το 3 είναι κατά προσέγγιση ο αριθμός του pi (π): (3.1415…)
[Η περιφέρεια του κύκλου είναι ελαφρώς περισσότερη από τρεις φορές όσο η διάμετρός του. Η ακριβής αναλογία ονομάζεται π.]
Είναι ο πρώτος μονός αριθμός μετά την μονάδα, και ο μόνος πρωταρχικός τριγωνικός αριθμός.
Το 3 είναι ο τέταρτος αριθμός της σειράς Fibonacci, συμπεριλαμβανομένου του 0
(ο οποίος σχηματίζεται από τους τρεις πρώτους αριθμούς: 0, 1, 1, 2, 3).

Είναι ο μικρότερος αριθμός πλευρών που μπορεί να έχει ένα απλό πολύγωνο:
ένα τρίγωνο.
Τρία από τα 5 πλατωνικά στερεά έχουν τριγωνικές όψεις: Τετράεδρον, οκτάεδρον, εικοσάεδρον.
Τρία από τα 5 πλατωνικά στερεά έχουν κορυφές όπου συναντώνται τρεις όψεις: Τετράεδρο, κύβος, δωδεκάεδρο.
Μόνο τρεις τύποι πολυγώνων περιλαμβάνουν τις όψεις των 5 πλατωνικών στερεών: Τρίγωνο, τετράγωνο, πεντάγωνο.

Τρία είναι ο πρώτος αριθμός που δηλώνει το σύνολο – αρχή, μέση και τέλος-.
Υπάρχουν τρία είδη τριγώνων – ισόπλευρα, ισοσκελή και σκαληνά .
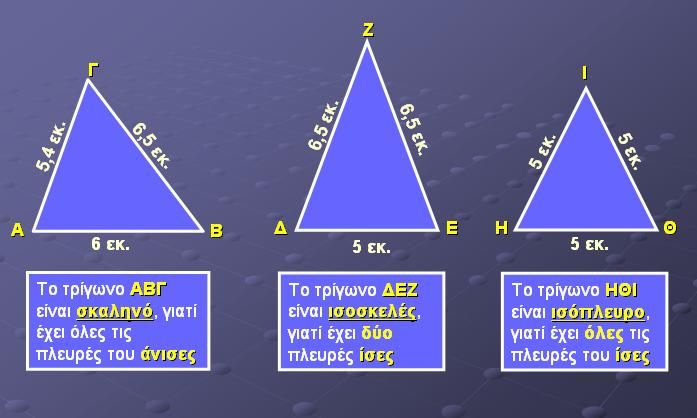
Υπάρχουν τρεις γωνίες –η οξεία, η αμβλεία, η ορθή.

Θα επανέλθουμε λίαν συντόμως για το 3 και τις τριαδικότητες του.
admin is | Topic: τριαδικότητες | Tags: None

No Comments, Comment or Ping
Reply to “Αριθμητικες ιδιοτητες της τριαδας”